Line Equations in Python

The other day I was playing with some Python challenges found on a popular sites, this challenge worked with xy coordinates on a 2D plane.

I wanted to show some of the code I wrote and how they work.

The Plane

Being the data is a tuple of x, y coordinates we will use the Cartesian Coordinate System .

I started my code off as a simple Python class:

class Line(object):

    def __init__(self, data):
            self.first, self.second = data

Using this Class I can input two points in a tuple like this:

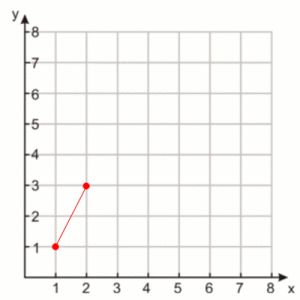
data = ((1,1), (2,3))

These coordinates would look like this on a 2D plane:

The Line

The coordinates ((1,1), (2,3)) holds quite a bit of data when it comes to the terms of Algebra.

Slope

The Slope of a line will tell us how steep it is, and can be calculated with the change in Y / change int X .

def slope(self):
        '''Get the slope of a line segment'''
        (x1, y1), (x2, y2) = self.first, self.second
        try:
                return (float(y2)-y1)/(float(x2)-x1)
        except ZeroDivisionError:
                # line is vertical
                return None

Using the slope method tells us this line has a slope of 2 .

>>> data = ((1,1), (2,3))

>>> line = Line(data)

>>> m = line.slope()

>>> print m
2.0

Y Intercept

The Y Intercept tells us at what point a line will meet the Y axis. To get a Y Intercept we use the equation b = y - mx where m is our slope .

def yintercept(self, slope):
        '''Get the y intercept of a line segment'''
        if slope != None:
                x, y = self.first
                return y - slope * x
        else:
                return None

And if we plug all our data back in we get a intercept of -1 :

>>> b = line.yintercept(slope)

>>> print b
-1.0

Solve for Y

Now that we know the slope of our line, and where our line meets the Y Axis we can plug in any X coordinate and solve for where Y will be:

def solve_for_y(self, x, slope, yintercept):
        '''Solve for Y cord using line equation'''
        if slope != None and yintercept != None:
                return float(slope) * x + float(yintercept)
        else:
                raise Exception('Can not solve on a vertical line')

And just like that we can when X is equal to 3 our Y will be 5 , just look at the graph above and imagaine.

>>> line.solve_for_y(3, m, b)
5.0

Solve for X

And lastly using our slope and Y intercept we can solve for X when Y is some value:

def solve_for_x(self, y, slope, yintercept):
        '''Solve for X cord using line equatio'''
        if slope != 0 and slope:
                return float((y - float(yintercept))) / float(slope)
        else:
                raise Exception('Can not solve on a horizontal line')

And we can do the reverse of above to verify they are both working, when X is equal to 5 our Y should be 3 :

>>> line.solve_for_x(5, m, b)
3.0

Put it all together

class Line(object):

    def __init__(self, data):
            self.first, self.second = data

    def slope(self):
            '''Get the slope of a line segment'''
            (x1, y1), (x2, y2) = self.first, self.second
            try:
                    return (float(y2)-y1)/(float(x2)-x1)
            except ZeroDivisionError:
                    # line is vertical
                    return None

    def yintercept(self, slope):
            '''Get the y intercept of a line segment'''
            if slope != None:
                    x, y = self.first
                    return y - slope * x
            else:
                    return None

    def solve_for_y(self, x, slope, yintercept):
            '''Solve for Y cord using line equation'''
            if slope != None and yintercept != None:
                    return float(slope) * x + float(yintercept)
            else:
                    raise Exception('Can not solve on a vertical line')

    def solve_for_x(self, y, slope, yintercept):
            '''Solve for X cord using line equatio'''
            if slope != 0 and slope:
                    return float((y - float(yintercept))) / float(slope)
            else:
                    raise Exception('Can not solve on a horizontal line')